1 08 2014

Bayramdan önceki birkaç gün ile bayramın son gününü saymazsak – ki, kâbus olduğuna şahidim –  şu günlerde İstanbul’da akan bir trafik ile karşı karşıyayız ve bu herkesin dudaklarında bir tebessüm vesilesi oluyor. Arabamızla hemen her yere rahatlıkla ve istediğimiz zamanda varmak gibi bir mutluluk yaşıyoruz – tabii, işe gidiş ve iş çıkış saatleri hariç. Ben şahit olmadım, ama bayram süresince bomboş bir İstanbul ile beraber olanlar mutlulukların doruğunu yaşamışlar. Yaşasın tatil ve yaşasın yaz tatili!

Araştırmacılık mesleğine ikinci kez giriş yaptığım ilk yıllarda – 1986 ya da 1987 yılı olmalı – İstanbul Metrosu için proje hazırlayan ABD kökenli bir danışmanlık şirketiyle toplantı yaparken, son derece sevecen ve konuşurken ağzından bal damlayan Mr.X – şimdi adını hatırlamam çok zor – yolculuk yapan insanlar ile trafikte seyreden araçların sayımı hakkında tecrübemiz olup olmadığını sorunca, o zamanlar PİAR’da – şimdiki TNS – birlikte çalıştığımız Ayşe Terek – şimdi Medran – ile birbirimize bakmış, ne diyeceğimizi düşünmeye başlamıştık ki, ben hemen atılarak, aslında bu konuda hayli tecrübeli olduğumu, öğrencilik yıllarımda Viyana Belediyesi için trafikte seyreden araçları sayan bir ekipte çalıştığımı söyleyivermiştim. Gerçekten de Viyana’da, Şilili bir arkadaşımın belediyeden aldığı ve sadece öğrencilerin çalıştığı bir iş için oluşturduğu ekipte uzunca bir süre çalışmış, ışık, hemzemin ya da alt – üst geçit olmayan birçok kavşakta sayım yapmıştım. İşi almıştık…

Bu meşakkatli işi daha sonra arkadaşım Işık Al – şimdi Pot – yürütmüştü. Akın Alyanak da projemizin direktörüydü. Müthiş bir iş yapmış, hemen hemen tüm İstanbul’da yapılan yolculukları ve trafikte seyreden araçları sayarak, şehrin trafik akım şemalarını çıkarmıştık. Muhtemelen İstanbul trafiği, bizim başlattığımız ve daha sonra devam bu araştırmalar üzerine tasarlandı.

Nitekim daha sonra Yöntem’i kurduğumda İstanbul Belediyesi’nden benzer proje talepleri gelmiş, ancak, karşımızda artık sevecen, ağzından bal damlayan ve bir o kadar da tecrübeli olan Amerikalı Mr. X olmadığı için söz konusu projeleri alabilme imkânı olmamıştı. Trafik meselesiyle tecrübelerim bununla sınırlı kaldı.

Depremler ve Norveç Fiyortları

Ta ki John Gribbin’in Derin Basitlik[1] ile Philip Ball’ın Critical Mass [2] adlı ilginç kitaplarını okuyana dek. Meraklılarına şiddetle tavsiye ederim.

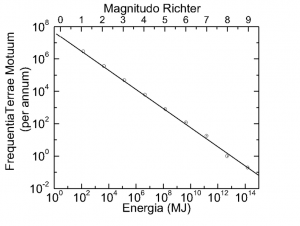
1906 yılında gerçekleşen Kalirforniya depreminden sonra bilimsel olarak ispatlanmıştır ki, çok sayıda küçük deprem ve çok az sayıda büyük deprem vardır. Örneğin 5 şiddetindeki her 1000 depreme karşılık 6 şiddetinde 100 deprem, 7 şiddetinde de 10 deprem vs. meydana gelmekteydi. Öte yandan depremlerin şiddetini ölçtüğümüz Richter ölçeği logaritmiktir ve ölçekteki bir birimlik artış açığa çıkan enerji miktarında 30 kat artışa karşılık gelir ve bu 2 şiddetindeki bir depremin 1 şiddetindeki bir depremden 30 kat daha güçlü olduğunu gösterir. 3 şiddetindeki bir deprem de 2 şiddetindeki bir depremden 30 kat, dolayısıyla 1 şiddetindeki bir depremden 900 kat daha güçlüdür.[3] Bu veriler ışığında ortaya çıkan ‘sıklık ve şiddet’ grafiği aşağıdaki gibi soldan sağa eğimli düz bir çizgi oluşturur. Buna, Gutenberg / Richter yasası denmektedir.

(Grafiğin üzerine tıklayınız)

Aslında, doğadaki fraktalleri[4], örneğin bir kıyı şeridinin uzunluğunu da örnek alarak, aynı biçimde ifade edebiliriz. Bu bağlamda, fraktale ilişkin özgün bir yapı sergileyen, yani, büyük fiyortların daha küçük fiyortlara ve küçüklerin daha da küçüklere ayrıldığı  Norveç Fiyortları iyi bir örnek olabilir. Şimdi, kıyı şeridinin fraktal boyutlarını tanımlamak için kıyının detaylı bir haritasını alıp özdeş kareler örgüsüyle kapladığımızı düşünelim. Yeterince büyük bir kare Norveç’in tamamını kaplamak için yeterli olacaktır. Kareleri küçültmeye başladığımızda ise kıyı şeridinin bükülen tüm koylarını kaplamak için sürekli daha fazla kareye ihtiyaç duyarız. Açıktır ki, kareleri yarı büyüklüğüne getirdikçe kaplama işini halledebilmek için evvelki kare sayısının iki katından fazlasına ihtiyaç duyarız. Karelerin boyutunun küçülmesine karşılık ihtiyacımız olan kare sayısındaki artışın hızı kıyı şeridinin fraktal boyutunu verir. İlginçtir ki, kareler küçüldükçe ölçülen kıyı şeridin uzunluğu artar, çünkü artık kıyı şeridindeki girinti ve çıkıntılar daha ayrıntılı olarak dikkate alınıyor demektir. Bu kez, log-log üzerinde gösterilen ‘uzunluk ve kare’ boyutu grafiği yine yukarıdaki gibi soldan sağa doğru eğimli düz bir doğru olur. Yani, değişim ölçüsünün büyüklüğü dışında yine Gutenberg / Richter yasasına benzer bir kuvvet yasasıyla karşı karşıya kalırız.

Şehirler ve Trafik Meselesi

Hepimizin bildiği gibi, dünyadaki tüm ülkelerde yüksek nüfuslu birkaç şehir ve daha küçük nüfuslu çok daha fazla sayıda şehir vardır. Ve yine bilimsel olarak ispatlanmıştır ki, farklı nüfuslardaki her şehir, nüfuslarıyla beraber bir log-log grafiği üzerinde kümelere ayrılır ve nüfuslarına karşılık gelecek biçimde yerleştirilirlerse düz bir doğru elde edilir. Yani, hem tüm dünya, hem de farklı bölgelerdeki insanların şehirlerde toplanışı bir kuvvet yasasına tabidir ve bu örüntü 1940’larda olduğu gibi şimdi de geçerlidir. Hepimiz nerede oturacağımıza bağımsız ve özgür irademizle karar veririz, ama depremlerin oluşumunu yöneten ya da fiyortların uzunluğunu ölçen yasaların  – ki, kuşkusuz daha birçok örnek vardır – aynısına tabi oluruz.

Şimdi tekrar başa dönebiliriz. Bugünlerde İstanbul’da akan trafiğe aldanmayalım, Eylül ayında yine yoğun bir trafikle karşılaşacağımız gün gibi aşikârdır. Hepimizin bildiği gibi trafik hafifken sorunsuz biçimde su gibi akar. Yoğunlaştıkça tıkanıklık alır başını gider. Sorun şudur: Bir araç herhangi bir nedenle  (muhtemelen önündeki araca çok yaklaştığından)  fren yaparsa, zincirleme bir etkiyle arkasındaki herkes yavaşlar ve – çok şükür ki yol güvenliği açısından – yavaşlamak hızlanmaktan daha kolay hale gelir.

Duisburg Üniversitesi’nde Kai Nagel ve Maya Paczuski tarafından 1995 yılında kurulan bir model ilginç sonuçlar doğurmuştur.[5] Tek sıra halindeki araçların, sollama olmaksızın tek yönlü bir yol üzerinde bulunduğu bu modelde tüm araçlar aynı boyutta olup, hızları bilgisayar simülasyonunda bir adımla sonraki adım arasında ne kadar hareket edebileceklerine göre belirleniyordu. Yani, bir araç önündekine çarpacak kadar hızlı gidiyorsa yavaşlamak, aradaki mesafe yeterinden fazla açıldıysa hızlanmak zorundaydı. Son olarak da, yavaşlamak hızlanmaktan daha kolay olacak şekilde, yavaşlama ve hızlanma becerilerinin ölçümü yapıldı. Model çalışmaya başladığında gerçek trafik tıkanıklıklarında rastlanan tüm davranışlar – trafik hafifken rahatça giden araçlar, yoğunken bazı tıkanıklıklar, kritik yoğunluk eşiği aşıldıktan sonra, yani çok yoğunken kâbus – ortaya çıkmıştı. Trafiğin ‘akış oranı ve yoğunluğunu’ gösteren grafik, kritik yoğunluk eşiğinden sonra, tıpkı Gutenberg / Richter ölçeğinde olduğu gibi soldan sağa düz eğimli bir doğruydu. Yani, trafiğe dahil olan araç sayısına göre ölçülen farklı yoğunluktaki tıkanıklıkların sayısı farklı şiddetlerdeki depremlerin sayısının tabi olduğu yasa ile aynıydı.

Özetlersem, öndeki araçlar hızla uzaklaşırken, gerçekte olduğu gibi daha fazla sayıdaki araç sıkışıkla karşılaştıkça fren yaptığından, yine gerçekte olduğu gibi tıkanıklık yüzünden trafiğin ortalama hızı düşünce öndekiler hızla gözden kaybolduğundan tıkanıklıklar trafiğin gerisine doğru ilerliyordu. Modelde, çeşitli tetiklemelere neden olan kaza, vb. dış faktör yoktu. Anlaşılacağı üzere eğer hız limiti düşürülürse hızlanmak ile yavaşlamak amacıyla fren yapmak için geçen zamanlar arasındaki farkın etkisi azalıyordu. Bunun anlamı şudur: Herkesin bildiği gibi, kalabalık bir otoyolda herkes hız limitlerine uyarsa, tüm insanlar varacakları yere, hızlı sürmeye çalışıp varacaklarından daha önce ulaşırlar.

* * *

İş yaşamamızda birkaç tane büyük, bundan biraz daha fazla sayıda orta büyüklükte, çok daha fazla sayıda da küçük işler yaparız; kuvvet yasası işlemeye devam eder yani. Başarı fenomenini alalım; hiç kimse sonsuza kadar başarılı olamaz. Olsa olsa, insanların birkaç büyük başarısı, bundan biraz daha fazla sayıda orta düzeyde başarısı, çok sayıda da küçük başarıları olur. Bakalım, kuvvet yasası cumhurbaşkanlığı seçimlerinde de kendini gösterebilecek olgunluğa erişti mi, erişmedi mi? Göreceğiz.

Notlar

ABD, Akın Ayanak, Araştırma, Ayşe Terek, Deprem, Fraktal, Gutenberg - Richter Yasası, Işık Al, İstanbul, İstanbul Belediyesi, İstanbul Metrosu, John Gribbin, Kai Nagel, Kaliforniya Depremi, kaos, Kuvvet Yasası, Mandelbrot, Maya Paczuski, Norveç Fiyortları, Philip Ball, PİAR, Richter Ölçeği, Şehir, TNS, Trafik, Viyana, Viyana Belediyesi, Yöntem Araştırma

Güle Güle Nimet Annem Entropik İşler